Part 1: Fun with Filters
Part 1.1 : Finite Difference Operator
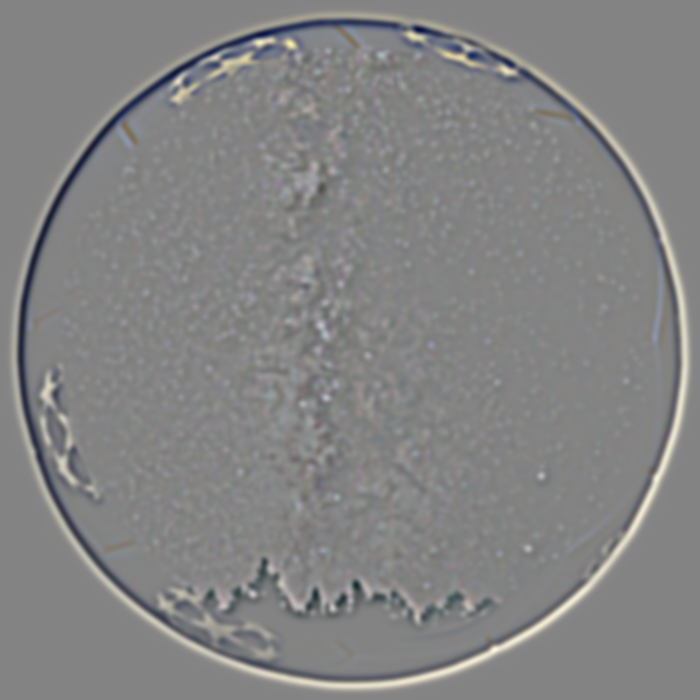
We applied the partial derivative in x and y direction where D_x = [1, -1] and D_y = [[1], [-1]]. Then we compute the gradient magnitude image by computing the sqrt((df/dx)^2 + (df/dy)^2) and then I binarize my image using the threshold to be 0.25 all the image will show below




Part 1.2 : Derivative of Gaussian (DoG) Filter
We applied the gaussian filter with kernel size 12 and the sigma to be 2 and then we applied the same partial derivative in x and y direction where D_x = [1, -1] and D_y = [[1], [-1]]. Then we compute the gradient magnitude image by computing the sqrt((df/dx)^2 + (df/dy)^2) and then I binarize my image using the threshold to be 0.05 all the image will show below. The difference from the first part is that the images are smoother and the gradient magnitude is more clear.





We can also get the same result by creating a derivative of the gaussian filter and then convolve the image. The result show below which we can see that the result is the same as above.







Part 2: Fun with Frequencies!
Part 2.1 : Image "Sharpening"
We applied the low pass filter then we subtract the low pass filter with kernel size 12 and sigma to be 2 from the original image to get the high pass filter. Then we add the high pass filter to the original image to get the sharpened image. We picked the alpha value to be 2.



Then we applied this technique to the the new image and then applied the same technique to the image where we use kernel size to be 12 and sigma is 2. Then we applied various alpha value to the image to see the different result.













Part 2.2 : Hybrid Images
We applied the low pass filter to derek image where we applied kernel size of 54 and sigma to be 9 and high pass filter we applied kernel size to be 36 and sigma to be 6 to the cat image. Then we add the two image together to get the hybrid image.





We then applied this technique to a few more pictures and we will use that in some case the hybrid image works but in some case it does not work where the last case is failed case.















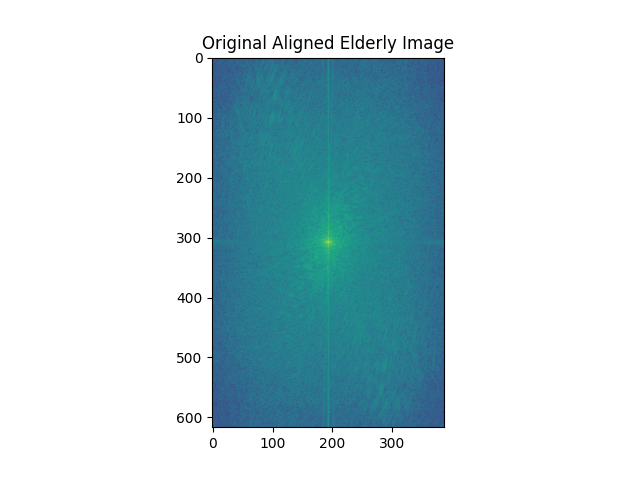
Then we show the log magnitude of the Fourier Transform of the two input images, the filter images and the hybrid image.
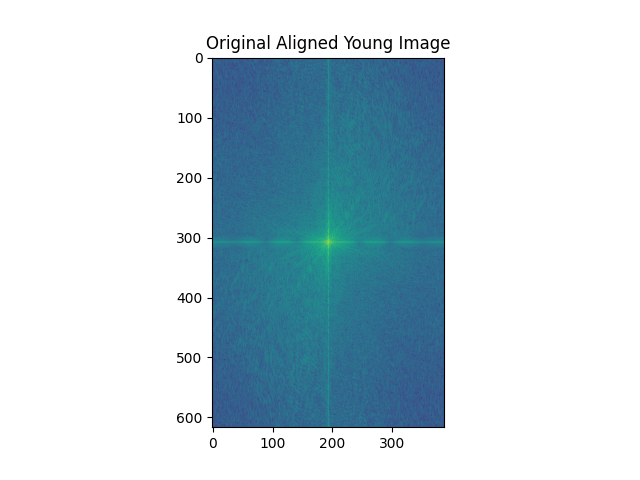
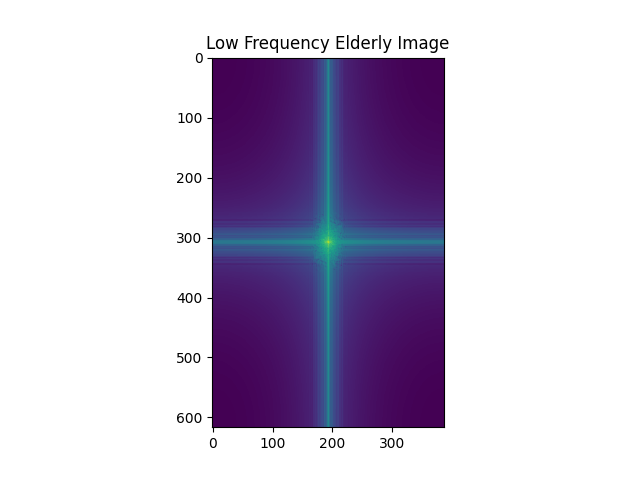
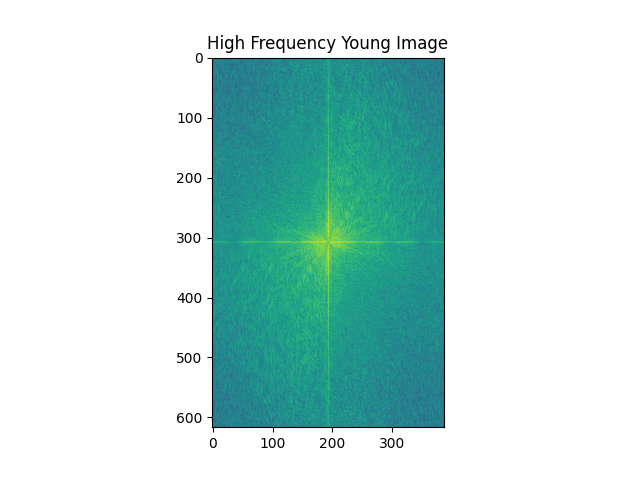
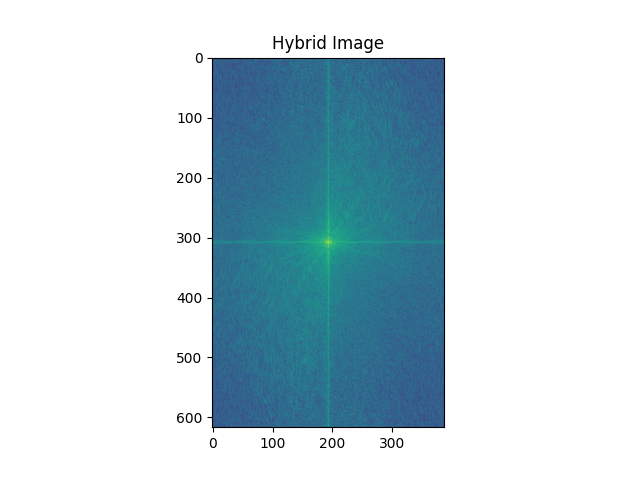
Part 2.3 : Gaussian and Laplacian Stacks
We implement a Gaussian and Laplacian stack and we apply it to the apple and orange image where we use kernel size to be 18 and sigma to be 3 for both of the images. We also apply the gaussian stack to the mask as well to get the blened image.



























Part 2.4: Multiresolution Blending
We applied the previous technique to two more images and we use kernel size of 18 and sigma to be 3 for both images.