CS 280A Project 4 : Image Warping and Mosaicing by Phudish Prateepamornkul

Part 1: Shoot the Pictures

We took a few images of the scenes around Berkeley campus and the images are show below

First Example First Image
First Example First Image
First Example Second Image
First Example Second Image
Second Example First Image
Second Example First Image
Second Example Second Image
Second Example Second Image
Third Example First Image
Third Example First Image
Third Example Second Image
Third Example Second Image
Fourth Example First Image
Fourth Example First Image
Third Example Second Image
Fourth Example Second Image

Part 2: Recover Homographies

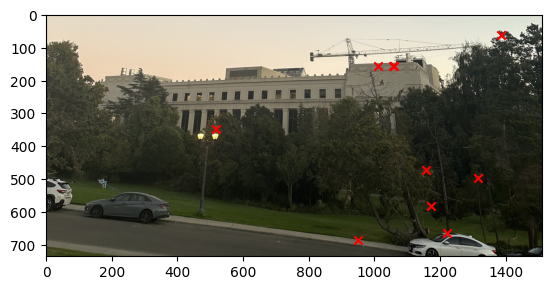
So the first thing we have to do is to find the correponding points between the images. This was done by using the tool from last year. Then we can use the corresponding points to find the homography matrix by using the least square method. This is done by using the equation that was set up in the class and the expandsion of the solution I look into Alec Li last year project. Specially, we need to find the homography matrix that map the source image to the target image and the equation is shown below.

\[ \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} wx' \\ wy' \\ w \end{bmatrix} \] \begin{align*} ax + by + c &= wx' \\ dx + ey + f &= wy' \\ gx + hy + 1 &= w \end{align*}

by substituing the value of w back into the equation we get the following equation.

\[ \begin{align*} ax + by + c &= (gx + hy + 1)x' \\ dx + ey + f &= (gx + hy + 1)y' \\ ax + by + c - gx'x - hy'x &= x' \\ dx + ey + f - gx'y - hy'y &= y' \\ \begin{bmatrix} x & y & 1 & 0 & 0 & 0 & -x'x & -x'y \\ 0 & 0 & 0 & x & y & 1 & -y'x & -y'y \end{bmatrix} \begin{bmatrix} a \\ b \\ c \\ d \\ e \\ f \\ g \\ h \end{bmatrix} &= \begin{bmatrix} x' \\ y' \end{bmatrix} \end{align*} \]

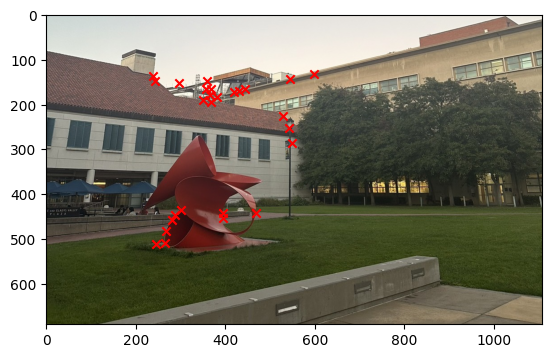
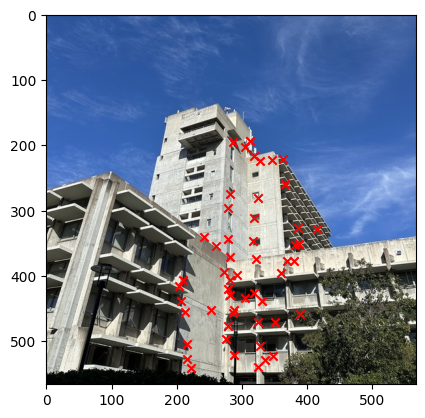
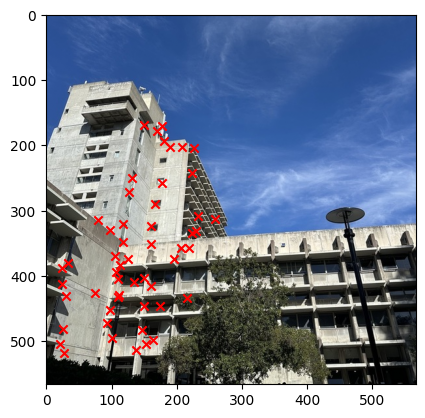
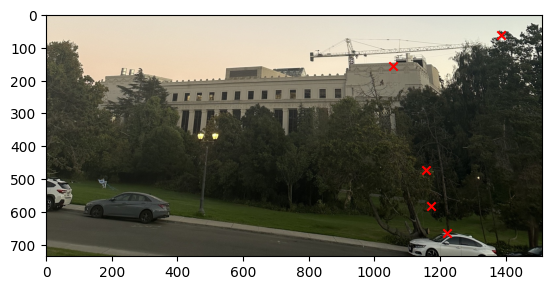
We can then stack all the points together and then use the least square method to solve for the homography matrix and get the solution. The image below show the result of correponding points for each image.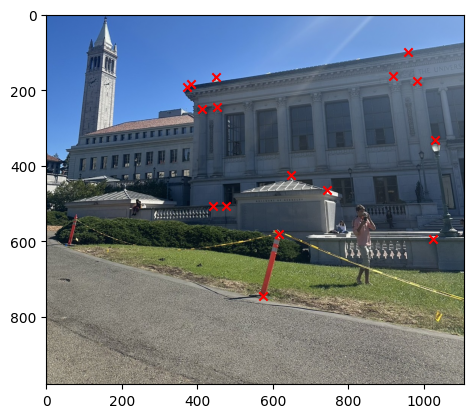

First Example First Image with Corresponding Points
First Example First Image with Corresponding Points
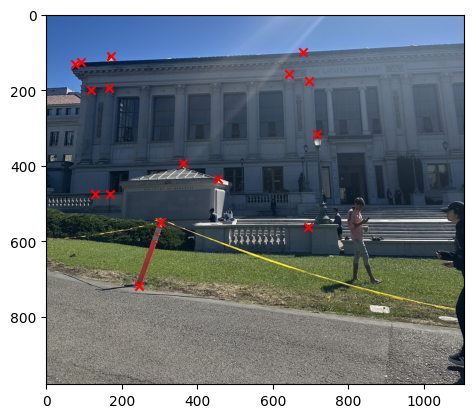
First Example Second Image with Corresponding Points
First Example Second Image with Corresponding Points
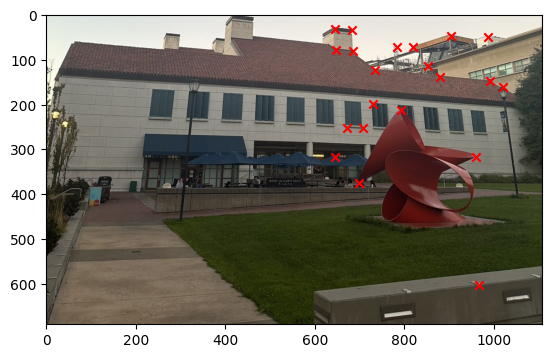
Second Example First Image with Corresponding Points
Second Example First Image with Corresponding Points
Second Example Second Image with Corresponding Points
Second Example Second Image with Corresponding Points
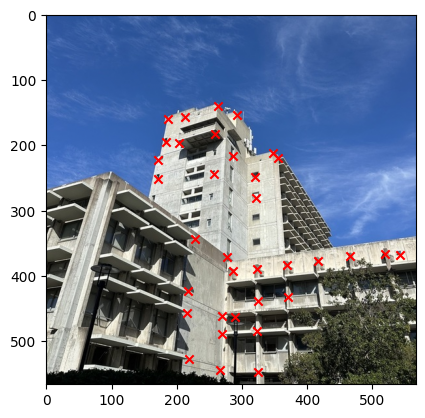
Third Example First Image with Corresponding Points
Third Example First Image with Corresponding Points
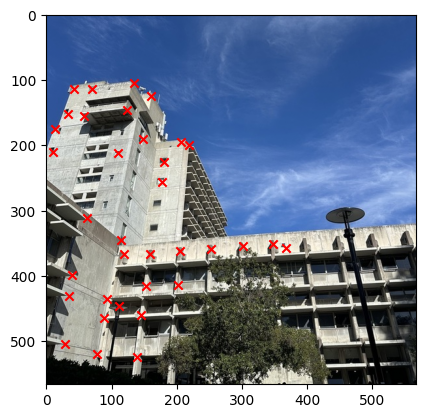
Third Example Second Image with Corresponding Points
Third Example Second Image with Corresponding Points
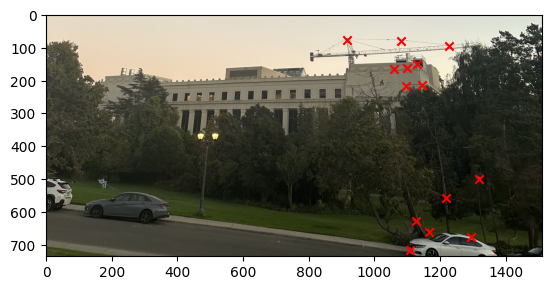
Fourth Example First Image with Corresponding Points
Fourth Example First Image with Corresponding Points
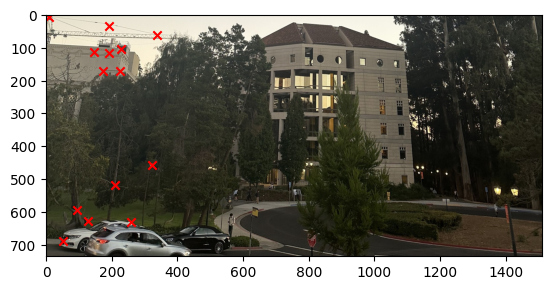
Fourth Example Second Image with Corresponding Points
Fourth Example Second Image with Corresponding Points

Part 3: Image Warping

Now that we have the homography matrix, we can use it to warp the image and this is done by firstly we have to map the corners of the source image to the target image so that we can find the size of the warped image. Then we have to get the new canvas where this is calculated from the target corners. Then we use something that is very similar to the previous project where we do the inverse warping and then use the grid data to get the pixel value and return the pixel value to the new canvas. The image belows show the result of the warped image where I warp the first image to the second and I also showed the second image warped to the first image as well.

First Example First Image Warped to Second Image
First Example First Image Warped to Second Image
First Example Second Image Warped to Fist Image
First Example Second Image Warped to Fist Image
Second Example First Image Warped to Second Image
Second Example First Image Warped to Second Image
Second Example Second Image Warped to Fist Image
Second Example Second Image Warped to Fist Image
Third Example First Image Warped to Second Image
Third Example First Image Warped to Second Image
Third Example Second Image Warped to Fist Image
Second Example Second Image Warped to Fist Image
Fourth Example First Image Warped to Second Image
Fourth Example First Image Warped to Second Image
Fourth Example Second Image Warped to Fist Image
Fourth Example Second Image Warped to Fist Image

Part 4: Image Rectification

Now that we have the homography matrix, we can use it to rectify the image. However, as we can see that there is only one image therefore I decided to define the corresponding points to the same image itself. The image below show the immediate result where the red points are representing the source point and the blue point represent where we want to map the source point to. Addtionally we also show the result of the rectified image. We note here that the first image is the photo I took by myself and the second image I got it from this website amazon package

First Example before rectification
First Example before rectification
First Example correponding points
First Example correponding points
First Example after rectification
First Example after rectification
Second Example before rectification
Second Example before rectification
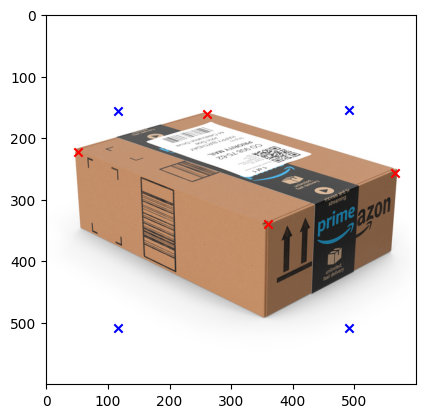
Second Example correponding points
Second Example correponding points
Second Example after rectification
Second Example after rectification

Part 5: Blend the images into a mosaic

Now that we have the homography matrix, we can use it to rectify the image. The first thing we have to do is that since the image that is being warped is not the same size as the sorce image, which therefore mean that we have to pad the image so that it is the same size and also we want to make sure that the image is also align with each other as well. Note that in our case we use the left image as the base and the right image to warp to the left image. The image below show the result of the padded image for each image and as we can see that the image is align and also same size.

First Mosaic First Image Padded
First Mosaic First Image Padded
First Mosaic Second Image Padded
First Mosaic Second Image Padded
Second Mosaic First Image Padded
Second Mosaic First Image Padded
Second Mosaic Second Image Padded
Second Mosaic Second Image Padded
Third Mosaic First Image Padded
Third Mosaic First Image Padded
Third Mosaic Second Image Padded
Third Mosaic Second Image Padded
Fourth Mosaic First Image Padded
Fourth Mosaic First Image Padded
Fourth Second Image Padded
Fourth Mosaic Second Image Padded

We then tried to use the mask in the lecture that is wherever there is only pixel from first image we set that to be 1 and whenever there are intersection between the two images then we set the mask to be 0. Then after that we do the interpolation of this mask with the base image and the warped image. The image below shows the result of both the mask and the mosaic image.

First Mosaic Mask
First Mosaic Mask
First Mosaic
First Mosaic
Second Mosaic Mask
Second Mosaic Mask
Second Mosaic
Second Mosaic
Third Mosaic Mask
Third Mosaic Mask
Third Mosaic
Third Mosaic
Fourth Mosaic Mask
Fourth Mosaic Mask
Fourth Mosaic
Fourth Mosaic

However, as we can see that the image is not as clear as it should be and also there seems to be some artifacts in the image. Therefore, we will try to fix this by using the bwdist function that was given in the lecture where we create the two mask base on the bwdist and then the last mask is the one such that the pixel value is closer to the first image. Then after that we used the gaussian pyramid to blend the image together and we show the final mask and also the final mosaic image.

Final First example first bwdist mask
Final First example first bwdist mask
Final First example second bwdist mask
Final First example second bwdist mask
Final First Mosaic Mask
Final First Mosaic Mask
Final First Mosaic
Final First Mosaic
Final Second example first bwdist mask
Final Second example first bwdist mask
Final Second example second bwdist mask
Final Second example second bwdist mask
Final Second Mosaic Mask
Final Second Mosaic Mask
Final Second Mosaic
Final Second Mosaic
Final Third example first bwdist mask
Final Third example first bwdist mask
Final Third example second bwdist mask
Final Third example second bwdist mask
Final Third Mosaic Mask
Final Third Mosaic Mask
Final Third Mosaic
Final Third Mosaic
Final Fourth example first bwdist mask
Final Fourth example first bwdist mask
Final Fourth example second bwdist mask
Final Fourth example second bwdist mask
Final Fourth Mosaic Mask
Final Fourth Mosaic Mask
Final Fourth Mosaic
Final Fourth Mosaic

Project 4B

For this part we will do feature matching for autostitching. We will start first with Harris Intterest Point Detector then we implement the Adaptive Non-Maximal Suppression and then we implement feature descriptor extraction then we implement the feature matching and at the end we use the RANSAC for more robust matching and then we make the image mosaic.

Part 1: Harris Interest Point Detector

I started to get the Harris Interest Point Detector by first using the code that was given. Where we set the edge discard to be more than 20. Then running the result on the image we get that there were too many points that were detected. Therefore, I decide to set a threshold for the corner response to be 0.1 and then we get that there are only about 11,000 points. The image below shows the result of the Harris Interest Point Detector.

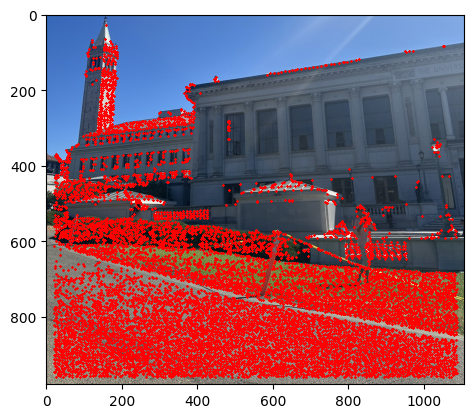
First Example First Image with Harris Points
First Example First Image with Harris Points
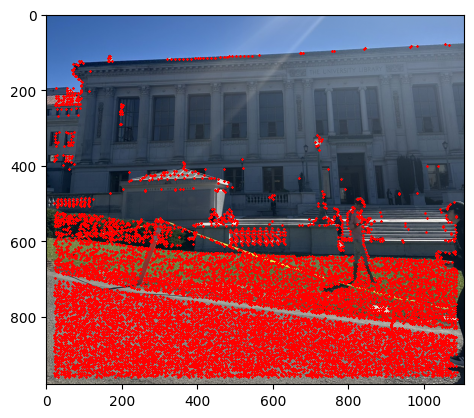
First Example Second Image with Harris Points
First Example Second Image with Harris Points
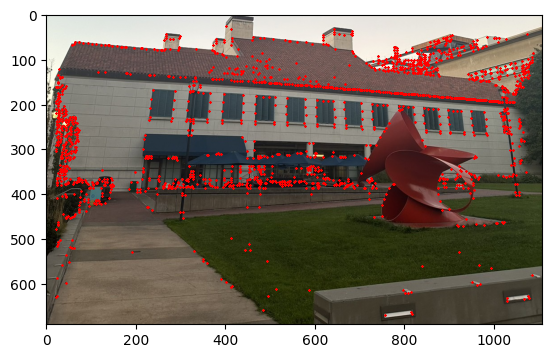
Second Example First Image with Harris Points
Second Example First Image with Harris Points
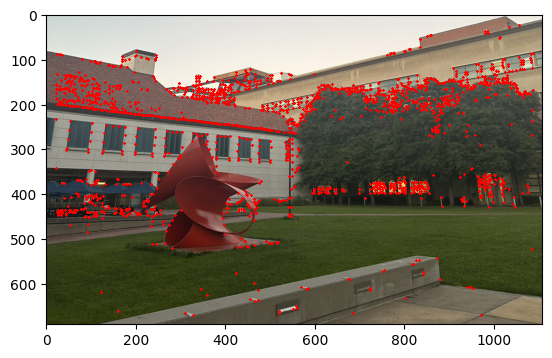
Second Example Second Image with Harris Points
Second Example Second Image with Harris Points
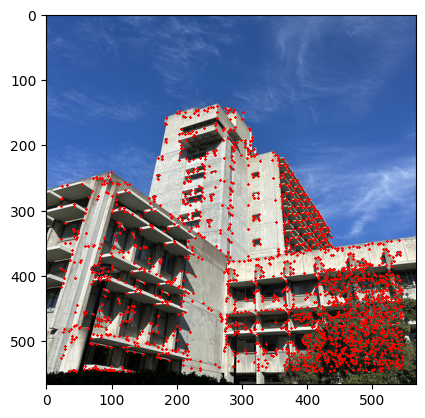
Third Example First Image with Harris Points
Third Example First Image with Harris Points
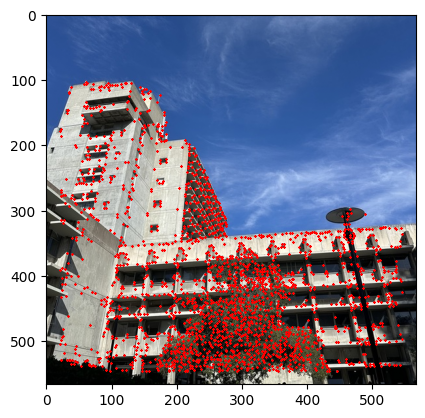
Third Example Second Image with Harris Points
Third Example Second Image with Harris Points
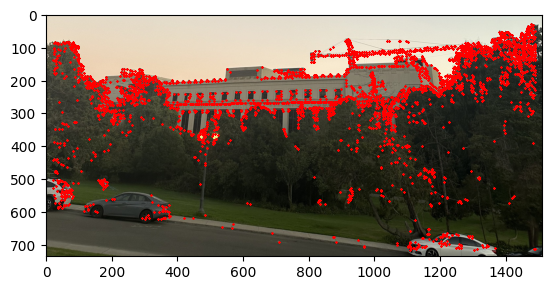
Fourth Example First Image with Harris Points
Fourth Example First Image with Harris Points
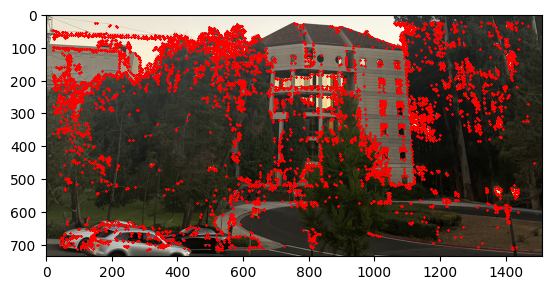
Fourth Example Second Image with Harris Points
Fourth Example Second Image with Harris Points

Part 2: Adaptive Non-Maximal Suppression

Now that we have the Harris Interest Point, we can see that there are still too many points that are detected. Therefore, we will still have to do the Adaptive Non-Maximal Suppression to filter the number of key points that we have. Essentially, the algorithm will assign every key point an r score where the function f is the corresponds to the corrner response. We have the following equation.

Here is the equation:

\[ r_i = \min_j |\mathbf{x}_i - \mathbf{x}_j|, \text{s.t. } f(\mathbf{x}_i) < c_{\text{robust}} f(\mathbf{x}_j), \mathbf{x}_j \in \mathcal{I} \]

Then we pick the 500 points that has the highest r scores as the output. The image below shows the result of the Adaptive Non-Maximal Suppression.

First Example First Image with Adaptive Non-Maximal Suppression
First Example First Image with Adaptive Non-Maximal Suppression
First Example Second Image with Adaptive Non-Maximal Suppression
First Example Second Image with Adaptive Non-Maximal Suppression
Second Example First Image with Adaptive Non-Maximal Suppression
Second Example First Image with Adaptive Non-Maximal Suppression
Second Example Second Image with Adaptive Non-Maximal Suppression
Second Example Second Image with Adaptive Non-Maximal Suppression
Third Example First Image with Adaptive Non-Maximal Suppression
Third Example First Image with Adaptive Non-Maximal Suppression
Third Example Second Image with Adaptive Non-Maximal Suppression
Third Example Second Image with Adaptive Non-Maximal Suppression
Fourth Example First Image with Adaptive Non-Maximal Suppression
Fourth Example First Image with Adaptive Non-Maximal Suppression
Fourth Second Image with Adaptive Non-Maximal Suppression
Fourth Example Second Image with Adaptive Non-Maximal Suppression

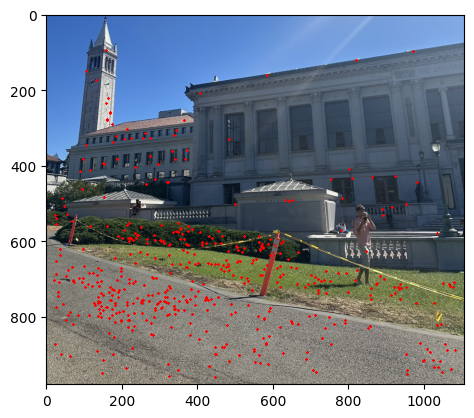
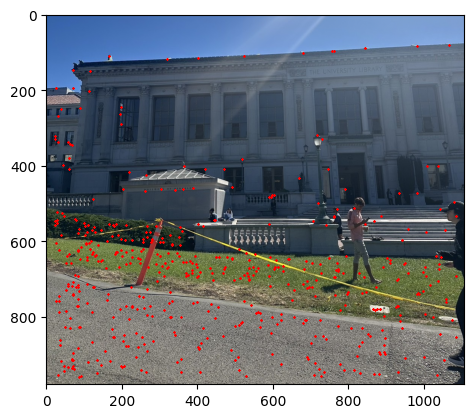
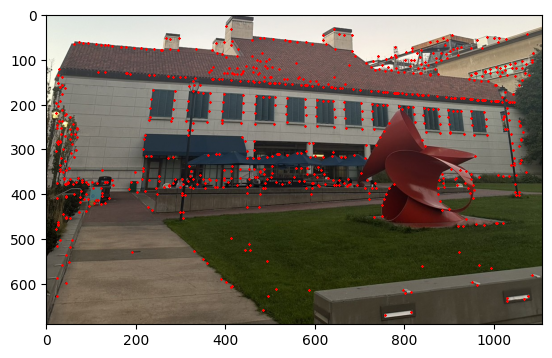
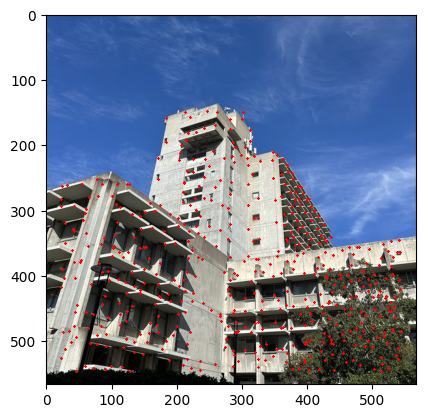
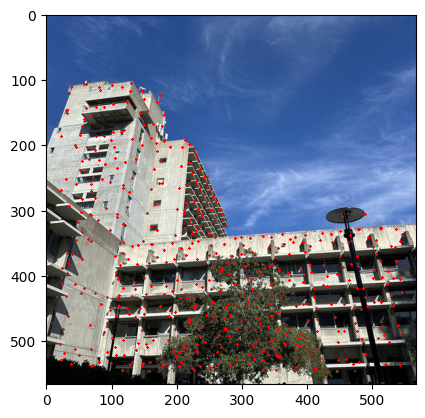
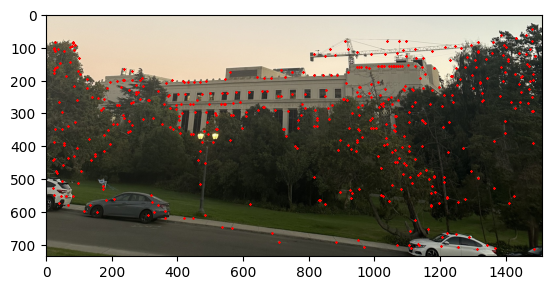
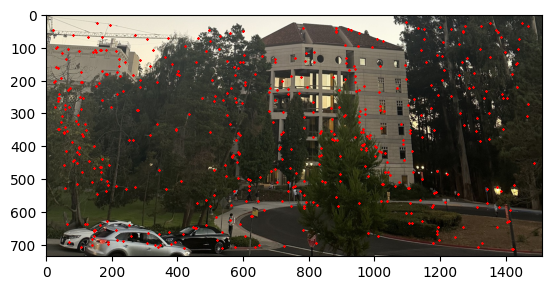
Part 3: Feature Descriptor Extraction

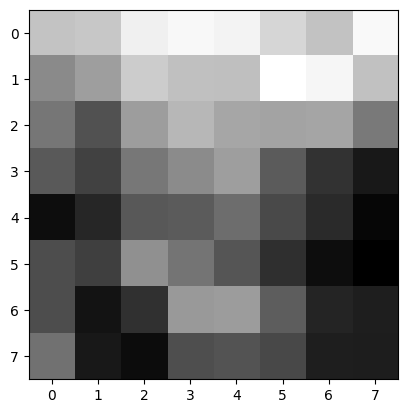
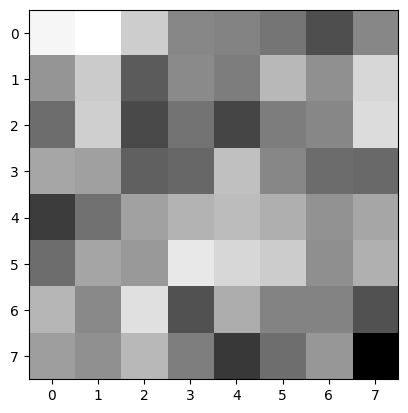
Now after we have the 500 points from the Adaptive Non-Maximal Suppression, we still need something more than just a single pixel of information. Therefore, we will look into extracting the local information about the image around the key points. We captured 40x40 patch center around each key point and then we downsampled this image to 8x8 patch and we also did the normalization of the image. The image below shows the result of the Feature Descriptor Extraction.

Example of Feature Descriptor
Example of Feature Descriptor
Example of Feature Descriptor
Example of Feature Descriptor

Part 4: Feature Matching

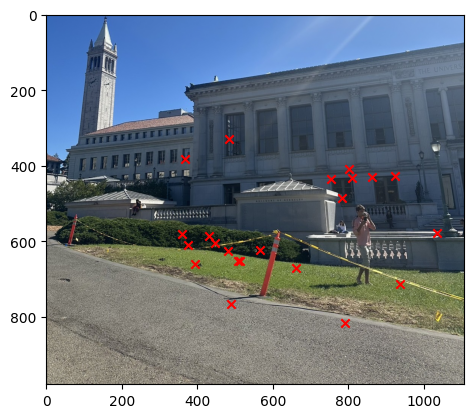
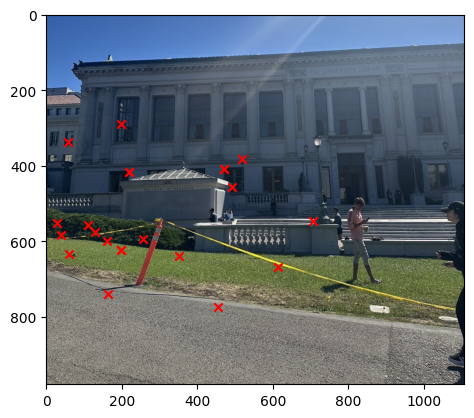
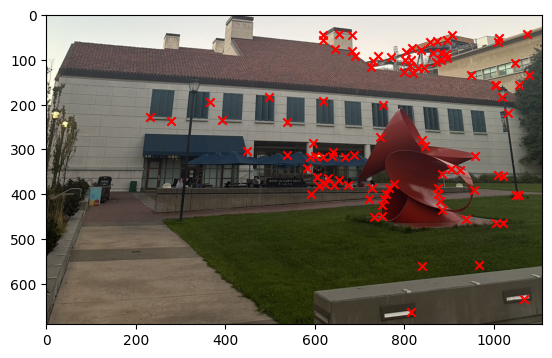
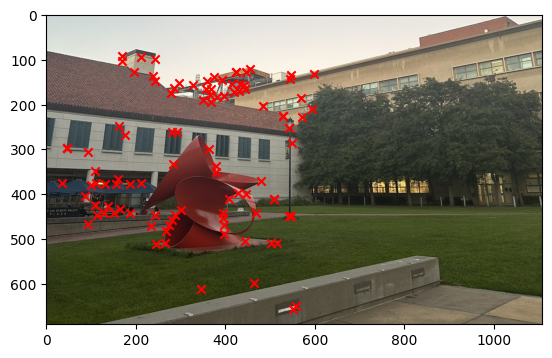
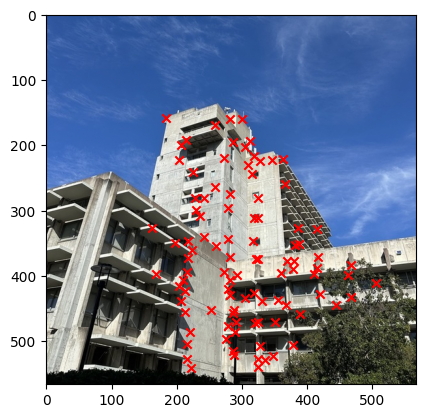
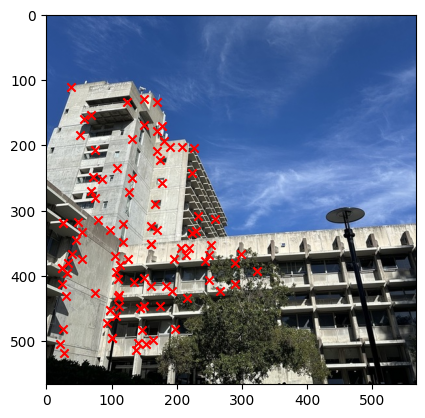
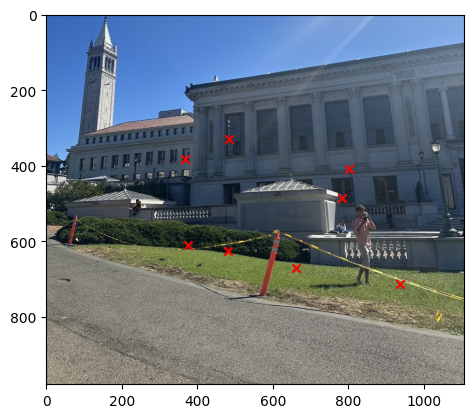
Once we get the image descriptor, then we have to use this to get the matched key points between the pairs of images. In order for us to do this, we have to use the L2 distance to find the closest key points between the two images using the Lowe's ratio. The Lowe's ratio is defined as the ratio of the distance between the closest key point and the second closest key point. If the ratio is less than 0.4 then we consider this to be a match. The image below shows the result of the Feature Matching.

First Example First Image with feature matching
First Example First Image with feature matching
First Example Second Image with feature matching
First Example Second Image with feature matching
Second Example First Image with feature matching
Second Example First Image with feature matching
Second Example Second Image with feature matching
Second Example Second Image with feature matching
Third Example First Image with feature matching
Third Example First Image with feature matching
Third Example Second Image with feature matching
Third Example Second Image with feature matching
Fourth Example First Image with feature matching
Fourth Example First Image with feature matching
Fourth Second Image with feature matching
Fourth Example Second Image with feature matching

Part 5: RANSAC

Now that we have the matched key points, we still do have that the there are still some outlier therefore we have to use the RANSAC to get the more robust matching. Using the following steps

The image below shows the result of the RANSAC.

First Example First Image with RANSAC
First Example First Image with RANSAC
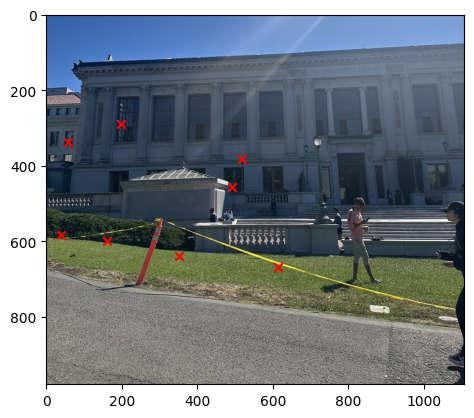
First Example Second Image with RANSAC
First Example Second Image with RANSAC
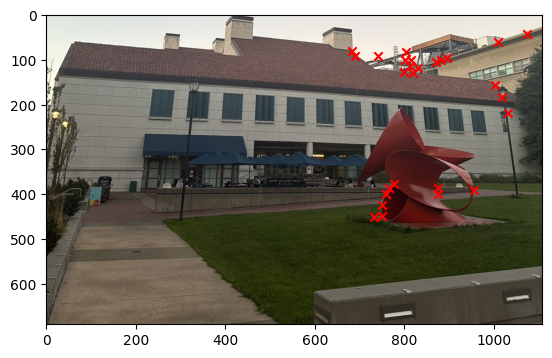
Second Example First Image with RANSAC
Second Example First Image with RANSAC
Second Example Second Image with RANSAC
Second Example Second Image with RANSAC
Third Example First Image with RANSAC
Third Example First Image with RANSAC
Third Example Second Image with RANSAC
Third Example Second Image with RANSAC
Fourth Example First Image with RANSAC
Fourth Example First Image with RANSAC
Fourth Example Second Image with RANSAC
Fourth Example Second Image with RANSAC

Part 6: Image Mosaic

We then use the same method as the previous part of the project to get the final mosaic image. The image below shows the result of the Image Mosaic.

First Example with Image Mosaic
First Example of Image Mosaic using Manual Correspondence
First Example with Image Mosaic
First Example Image Mosaic using Auto Correspondence
First Example with Image Mosaic
Second Example of Image Mosaic using Manual Correspondence
First Example with Image Mosaic
Second Example Image Mosaic using Auto Correspondence
First Example with Image Mosaic
Third Example of Image Mosaic using Manual Correspondence
First Example with Image Mosaic
Third Example Image Mosaic using Auto Correspondence
First Example with Image Mosaic
Fourth Example of Image Mosaic using Manual Correspondence
First Example with Image Mosaic
Fourth Example Image Mosaic using Auto Correspondence

What have you learned ?

The thing I have learned from this project is how can I was able to use linear algebra to get the homography matrix and then use it to create the mosaic image which is a very interesting thing that we can do from a simple linear algebra.